|
5 Die Elektronenhülle
5.1 Die Energieunterschiede der
Elektronenbahnen
Eine Konsequenz der direkten Synchronisation
der Elektronenbahnen mit den Protonen sind die bekannten
Energieverhältnisse stabiler und emittierender Bahnen.
Die Umlauffrequenz des Elektrons der Bahn n
sei fn (n=1,2,3...). Die Frequenz der Bahn 0 ist
gleich f1. Da das Elektron der lose gekoppelten Bahn 0
und der fest synchronisierten Bahn 1 im stabilen Zustand durch das
Proton phasenstarr synchronisiert wird, ist anzunehmen, dass die höheren
Bahnen ebenfalls einen synchronisierten Zustand höherer Ordnung
einnehmen.
|
Das bedeutet: |
|
fn |
= |
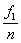 (6)
(6) |
Für f0 gelten die,
makroskopisch vergleichbaren, Keplerschen Planetengesetze. Für f1
bis fn gilt
|
|
|
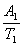 |
= |
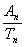 (7). (7). |
Die Geschwindigkeitskopplung für die
stabilen Elektronenbahnen lautet
|
|
|
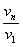 |
= |
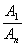 (8).
(8). |
Das bedeutet aber, dass der Umfang aller
Bahnen 1 bis n gleich sein muss. Aus diesen Betrachtungen folgt der
Verlauf der Bahnen im Wasserstoffatom im Bild 5.1, wobei das Proton mit
- dargestellt ist.
|
Bild 5.1: Bahnen eines Hüllenelektrons des H-Atoms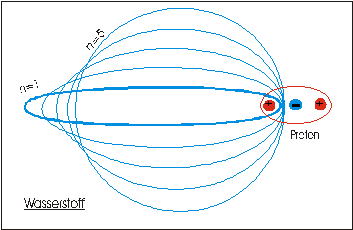 |
Die Bahn n=1 wird
von jedem, n=2 von jedem zweiten, n=3 von jedem dritten
Ladungswechsel im Proton synchronisiert. |
Alle höheren Bahnen n (fn> f0)
verlaufen durch das Proton - nur diese sind stabil. Die Bahn n=1 wird
von jedem, n=2 von jedem zweiten, n=3 von jedem dritten Ladungswechsel
im Proton synchronisiert.
Das Elektron wird durch das innenliegende
Positron auf die in (6) angegebene Frequenz synchronisiert. Für die
Umlaufzeit Tn gilt
|
|
|
Tn |
= |
n×T1
(9). |
|
Aus (6) und (7) folgt |
|
An |
= |
n×A1 (10). |
|
(10) in (8) ergibt |
|
vn |
= |
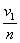 (11).
(11). |
|
Nach |
|
E |
= |
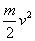 folgt folgt |
|
|
|
En |
= |
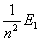 |
Alle so im Proton synchronisierten Bahnen n
haben exakt 1/n2 mal so viel Energie wie die erste Bahn, was
die praktischen Messungen bestätigen. Das Modell und der Rechenweg ist
für alle stabilen Elektronenbahnen aller Elemente gültig. Bei
höherwertigen Elementen ist die Synchronisation der Bahnen n>1 durch
benachbarte Protonen möglich.
5.2 Die Spektrallinien
Ein Elektron strahlt im Normalfall bei jedem
Umlauf Energie ab. Die stabile Bahn ist mit der des zugehörigen
Positrons gleichsinnig. Jeder Geschwindigkeitsverlust führt zu einer
Beschleunigung durch das Positron auf Kosten der im Proton ablaufenden
Zeit. Das bedeutet, dass sich die großen Halbachsen weniger
gegeneinander verdrehen. Die eigentliche Energie des Atoms steckt vor
allem in der relativistischen Zeitdilatation des Atomkernes.
Durch kleine Energiezufuhr wird die Form der
Elektronenbahn geändert, jedoch nicht deren Gesamtfläche und Frequenz.
Die überhöhte Geschwindigkeit wird bei jeder Begegnung mit einem
Positron abgebremst. Wird die Geschwindigkeit zu groß, ändert sich die
Form der Bahn innerhalb zweier Umläufe. Die Fläche und die Umlaufzeit
wird genau n mal so groß, je nach Bahnnummer. Das bewegte Elektron
strahlt weiter Energie ab, wobei das Verhältnis von Fläche und
Umlaufzeit konstant bleibt. Dabei verlängert sich die Halbachse der Bahn
solange, bis die zunehmende Beschleunigung zu genau einem Umlauf auf
einer niederen Bahn führt. Die Geschwindigkeit ist aber bei Ankunft am
Kern noch so klein, dass es sofort wieder auf die höhere Bahn gelangt.
Das Elektron wird nach jedem Umlauf im Wechsel auf die höhere Bahn
abgebremst oder auf die niedere beschleunigt. Das bedeutet, dass die
Energie der einen Bahn positiv und die andere negativ ist. Die Energie
dieses Zustandes entspricht also genau der Differenz der Energie der
einen Bahn und der anderen. Während der Umsynchronisation wechselt also
das Elektron nach jedem Umlauf die Bahn, wobei diese sich sehr in ihrer
Exzentrizität unterscheiden. Das bevorzugt die Abgabe eines Photons der
Energiedifferenz der beiden Bahnen. |