|
Physik |
Die „klassische“ Quantenphysik Olaf
Böttcher, 07.07.2012
Der Zufall muss nicht mehr bemüht werden. Es ist
eine Theorie entstanden, die alle quantenphysikalischen Vorgänge auf
klassische Art erklärt. Aus diesen Betrachtungen wird klar, dass die
physikalischen Effekte wesentlich intensiver und exakter quantisiert
sind, als es sich mit den bisher existierenden Theorien erkennen lässt.
Grundlage sind wenige lokale subatomare Vorgänge. Diese sind für das
Zusammenspiel der Elementarteilchen im Atom über die makroskopische
Physik bis hin zur kosmologischen Gravitation ursächlich. In dieser
kurzen Einführung sind die anschaulichen Herleitungen und die exakten
Berechnungen der Feinstrukturkonstante und des Massendefektes
hervorgehoben.
1. Ausgangspunkt
2. Die Bahn des Elektrons
3. Das
Energieniveauschema
4. Die Coulomb Kraft im Kern
5. Proton Neutron
Massendefekt
1. Ausgangspunkt
1911 war nach den Experimenten von
Rutherford klar, dass das Atom aus einem sehr kleinen, massereichen Kern
positiver Ladung und einer Hülle negativer Elektronen mit wesentlich
geringerer Masse besteht. Damals war bereits durch Plancks geniale
Schlussfolgerungen bekannt, dass Materie Energie nicht kontinuierlich
sondern in Quanten abstrahlt.
Wahrscheinlich weil diese Gedankengänge zu
neu und faszinierend waren, hat sie keiner bis zur letzten Konsequenz
durchdacht. In den Köpfen wurde Bohrs Atommodell anerkannt, ganz einfach
weil es schön war und nicht die unlösbar erscheinenden Probleme
enthielt, die beim Sturz des Elektrons in den Kern zu befürchten waren.
Jeder wusste, dass die Elektronen unter allen denkbaren Umständen, von
sämtlichen möglichen Bahnen in den Kern stürzen. Alle wollten das nicht
wahr haben, warum auch immer.
Ähnliches passierte der
Relativitätstheorie durch vergleichbare Hintergründe. Die Elektronen auf
den Bohrschen Bahnen waren so langsam, dass Einsteins geniale Theorie
nicht bemüht werden musste. Die Kerne wurden als träge ruhende Masse
betrachtet. Dazu gesellte sich Heisenbergs faszinierende
Unschärferelation. Durch deren raffinierte Mathematik wurde es unnötig,
nach Kleinerem oder Exakterem zu suchen, ganz einfach weil dort nichts
mehr sei. Wie so oft haben sich die hartnäckig angebrachten Argumente
durchgesetzt, nicht die logischen.
Ungeachtet aller anderen
Ungereimtheiten will keiner aussprechen, dass das Neutron vielleicht
doch nichts anderes als ein Proton mit zusätzlichem Elektron ist. Diese
Annahme hat sich schon vor der Entdeckung des Neutrons nicht durchsetzen
können, da das bereits damals den akzeptierten Irrtümern widersprach. In
den zwanziger Jahren stellte sich heraus, dass der Kern nicht nur aus
Protonen bestehen kann. Es wurde intensiv ein Modell in Betracht
gezogen, nach dem der Kern aus mehr als der der Ladung entsprechenden
Anzahl von Protonen besteht und diese durch die entsprechende Anzahl
Elektronen neutralisiert werden. Das entsprach bereits mehr der Realität
als alle heute existierenden Theorien.
1913 hat Bohr den Atomdurchmesser
zu etwa 1x10-8 cm festgestellt. Egal welche Kreisbahn oder Sommerfeldsche Ellipse angenommen wurde, das Elektron muss aus den
bekannten Gründen zum Kern stürzen. Nach dieser Begegnung kann es nur
wieder bis zur angenommenen Atomoberfläche, dem Startpunkt des Sturzes
gelangen, um erneut abzustürzen. Anfang der zwanziger Jahre des
vergangenen Jahrhunderts waren so viele Eigenschaften des Atoms
bekannt, dass nur noch eine mögliche Bahn übrig blieb, nämlich die, von
der niemand etwas wissen wollte.
2. Die Bahn des Elektrons
Gehen wir
erst einmal vom Wasserstoffatom aus. Das Elektron befindet sich im
Abstand von etwa 0,5x10-8 cm vom Kern am Umkehrpunkt seiner Bahn einen
Moment in Ruhe. Das Proton stellen wir uns für diese Betrachtung vorerst
als Kugel mit dem Durchmesser von 10-13cm vor. Am Umkehrpunkt wird das
Elektron durch die Coulombkraft in Richtung Kern beschleunigt, und zwar
an dieser Stelle mit etwa 1023 ms-2. Die Beschleunigung nimmt ständig zu
und das Elektron erreicht mit nahezu Lichtgeschwindigkeit den
unmittelbaren Bereich des Kernes, die gedachte Kugeloberfläche. Was dort
genauer passiert wird an späterer Stelle beschrieben, erst einmal
soviel: Es umläuft einen positiven Teil des Protons innerhalb der Kugel,
um sich dann wieder vom Kern zu entfernen. Dabei bewegt es sich nicht
zwingend in die Richtung, aus der es gekommen ist, sondern in irgendeine
andere. Das Elektron hält sich so am häufigsten in einer Entfernung von
0,5x10-8 cm vom Proton mit der Geschwindigkeit v = 0 auf, nach jedem
Fall aber an einer anderen Stelle einer gedachten Kugeloberfläche um das
Proton.
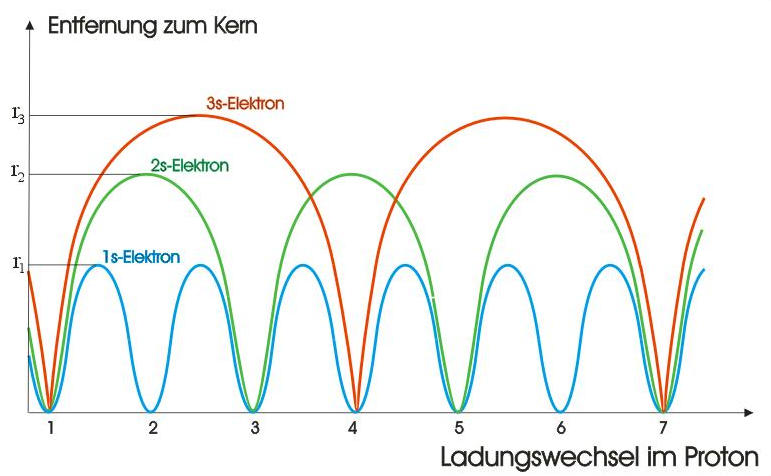
Für alle Elemente
gilt, dass dieser Vorgang als elastischer Stoß am Kern betrachtet werden
kann mit dem enorm wichtigen Zusatz, dass dabei das Elektron von einem
exakten Takt des Protons synchronisiert wird. Durch diese
Synchronisation ist der konstante Durchmesser der Atome gegeben. Mit
einer für jeden Kern eigenen Frequenz bewegt sich ein Positron aus jedem
Proton an die Kernoberfläche und wieder zurück. In diesem Moment wird es
von dem Elektron der Hülle umlaufen. Kommt das Elektron zu spät an, weil
der Abstand etwas größer war ist das Positron bereits auf dem Rückweg in
den Kern.
Durch den vorher
größeren Abstand und die damit länger anhaltende Beschleunigung ist das
Elektron zu schnell, die Geschwindigkeiten subtrahieren sich, es wird
abgebremst und entfernt sich nicht mehr soweit wie beim vorherigen Fall.
Kommt es zu früh an, also aus geringerer Entfernung und deshalb zu
langsam, addieren sich die Geschwindigkeiten, da sich das Positron noch
in Richtung Kernoberfläche entgegen dem Elektron der Hülle bewegt. Das
wird beim Umlauf beschleunigt, um sich mit größerer Geschwindigkeit
wieder etwas weiter vom Kern zu entfernen. Dieser Vorgang entspricht
einer festen Phasensynchronisation. Der Takt des Protons bestimmt somit
den Atomdurchmesser.
3. Das Energieniveauschema
Wieder vom
Wasserstoff ausgehend:
Für den Bohrschen
Radius ergibt sich für den äußeren Betrachter eine Taktfrequenz im
Proton von etwa 1,6x1016 Hz. Das Geschilderte entspricht der Bahn n=1.
Wird dem Elektron so viel Energie zugeführt, dass es jedes Mal später
und dementsprechend schneller am Kern ankommt, wird es dann wenn es nach
der Mitte des folgenden Taktes ankommt von jedem zweiten Takt des
Protons nach gleichem Prinzip synchronisiert.
Das Elektron
befindet sich auf n=2, der Umkehrpunkt liegt etwa 1,5 mal so weit vom
Kern entfernt wie bei n=1. Ein Fall dauert genau doppelt so lang wie bei
n=1. Die Geschwindigkeit ist beim Umlauf um das Positron genau so groß,
dass es entsprechend weit vom Kern den Umkehrpunkt erreicht und nach
zwei Takten wieder am Kern erscheint. Die Hauptquantenzahl n=3 bedeutet,
dass bei jedem dritten Takt synchronisiert wird, die Bahn n=4 bei jedem
vierten.
Stürzt ein
Elektron aus großer Entfernung auf ein freies Proton, kommt es dort mit
etwa c an. Wird es beim Umlauf um das Positron innerhalb der gedachten
Kernoberfläche so stark abgebremst, dass es sich nur wieder bis zum
Bohrschen Radius entfernt, wird es sofort auf Bahn n = 1
synchronisiert. Dafür emittiert das Atom ein Photon der Energie 13,6eV.
Diese Energie wird dem Elektron während des Umlaufs im Proton als
kinetische Energie entzogen – wie, das wird später beschrieben. Seine
Geschwindigkeit sinkt um vi = 2,19x106 m/s. Das Elektron bewegt sich
auf dem Bohrschen Radius zwischen Kern und Atomoberfläche, wo es wie
oben beschrieben am Bahnumkehrpunkt die Geschwindigkeit v = 0 hat. Wird
das Elektron auf der Bahn n=1 durch ein Photon der Energie 13,6 eV
beschleunigt, hat es an der Oberfläche noch die Geschwindigkeit vi =
2,19x106 m/s. Das Elektron besitzt mit vi genau die notwendige
Fluchtgeschwindigkeit, um wieder im Unendlichen zu verschwinden. Das
Verhältnis der Fluchtgeschwindigkeit zur Lichtgeschwindigkeit ist exakt
die Sommerfeldsche Feinstrukturkonstante α (≈1/137), α=
vi/c
Wird ein aus
großer Entfernung am Proton ankommendes Elektron beim Kerndurchlauf so
abgebremst, dass es sich zunächst auf der Bahn n=2 aufhält, also bei
jedem zweiten Takt synchronisiert wird, hat sich seine Geschwindigkeit
um v = 1,1x106 m/s verringert, während ein Photon mit E=3,4eV auf den
Weg geschickt wird. Befindet sich dieses Elektron mehrere Takte auf der
Bahn n=2 und gibt mehr und mehr Energie ab, kommt es immer eher vor
jedem zweiten Takt des Protons an. Die Beschleunigung reicht nicht mehr
aus, um auf der Bahn zu bleiben. Ab einer bestimmten Periode ist es
plötzlich am späten Ende des jeweils folgenden Taktes am Proton. In
diesem Moment wird dem Elektron die Energie von 10,2eV entzogen, diese
Energiedifferenz hat das abgestrahlte Photon. Das Elektron ist auf Bahn
1 synchronisiert.
Die
Hauptquantenzahl n bedeutet also, dass bei n=1 das Elektron mit jedem
Takt, bei n=2 mit jedem 2. Takt, bei n=3 mit jedem 3. Takt usw. am Kern
synchronisiert wird.
Die
Nebenquantenzahl l (s, p, d, f ): Die Elektronen der Bahnen n=2 werden
bei jedem 2. Takt synchronisiert. Für die beiden möglichen s-Elektronen
erfolgt die Synchronisation mit T1, T3, T5 usw., für die p-Elektronen
mit den Takten T2, T4, T6 ….Auf den Bahnen n=3 werden die s-Elektronen
entsprechend mit T1, T4, T7, T10 usw. synchronisiert, die p-Elektronen
mit den Takten T2, T5, T8, T11 und die d-Elektronen mit T3, T6, T9, T12
… Analoges gilt für die Bahnen der höheren Elemente. Die f-Elektronen
werden von T4, T8, T12 usw. synchronisiert.
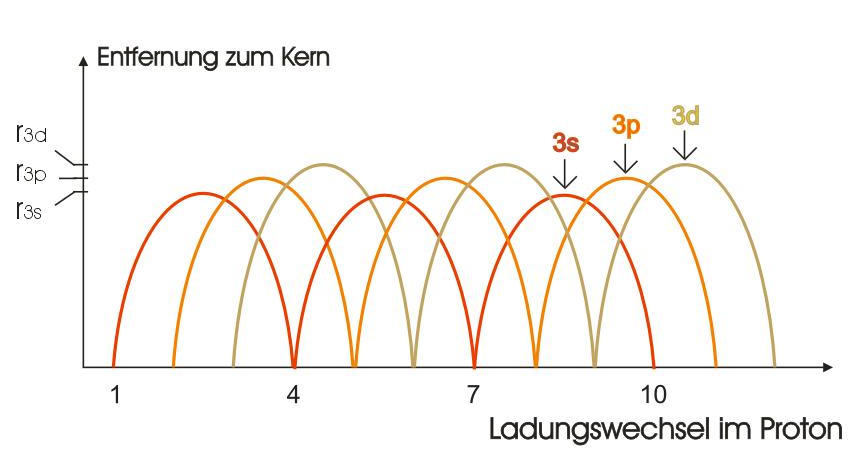
Die
Magnetquantenzahl
Die bisher
beschriebenen Eigenschaften der Elektronenbahnen ergeben die bekannten
räumlichen Orientierungen.
Die
Spinquantenzahl
Der Spin des
Elektrons entsteht durch einen relativistischen Effekt. Durch die großen
Geschwindigkeitsunterschiede von 0 bis annähernd c ergibt sich während
des Umlaufs um das Positron an der Kernoberfläche, also während sich
Positron und Negatron nahe sind eine Zeitdilatation. Analog zu der
Sonnennähe der Planeten bezeichnen wir diesen Bereich der Nähe der
Elektronen als Periel. Für den äußeren Betrachter verläuft hier die Zeit
im Elektron langsamer. Nach Kepler ergibt sich eine Perieldrehung, die
einer Drehung, also einem Winkel der Elektronenbahn vor und nach einer
Synchronisation entspricht. Für das Wasserstoffatom mit dem niedrigsten
Energieniveau bedeutet das: Nach jeder Synchronisation entfernt sich das
Elektron vom Kern bis zum Bohrschen Radius auf der annähernd geraden
Bahn B(x). Es gelangt auch auf B(x) wieder zum Kern und wird dort
synchronisiert. Es entfernt sich wieder vom Kern bis zum Atomradius,
jedoch auf der Bahn B(x+1). Durch die Perieldrehung während der
Synchronisation liegt zwischen B(x) und B(x+1) ein Winkel. So verlaufen
alle Bahnen B(x+n) nadelförmig vom Kern ausgehend gleichmäßig um das
Proton verteilt. Die Aufenthaltswahrscheinlichkeit des Elektrons ist am
häufigsten in der Nähe der Kugeloberfläche mit Bohrschem Radius um den
Kern, da dort dessen Geschwindigkeit am geringsten ist.
Die
verhinderte Perieldrehung
Für den äußeren
Betrachter wirkt in einem höherwertigen Atom oder Molekül auf ein
Elektron in Kernnähe eine relativistische Zeitdilatation. Die dadurch
angestrebte Drehung der Halbachsen der Bahn wird durch die anderen
Elektronen des Atoms und durch die Bindung zu umliegenden Atomen gehemmt
oder verhindert. Dadurch existiert für das Elektron in Kernferne ein
Geschwindigkeitsüberschuss. Der Synchronisationsvorgang am Kern sorgt je
nach Phasenlage für eine positive oder negative Beschleunigung des
Elektrons in Kernnähe. Das führt zu einer stabilen Bahn. Dieser Effekt
ist im Proton wesentlich stärker ausgeprägt.
4. Die Coulomb Kraft im
Atomkern
Nach der
Entdeckung der Radioaktivität wurde klar, dass die Wirkung der im Kern
vorhandenen Kräfte um mehrere Zehnerpotenzen stärker ist als die
Coulombkraft in vergleichbaren Dimensionen. So schloss man auf die
Existenz einer völlig anders gearteten Grundkraft, der starken
Kernkraft. Tatsächlich wird aber die Wirkung der elektrostatischen
Anziehung und Abstoßung im Atomkern verstärkt. Wie, das kann anhand der
inneren Struktur von Proton und Neutron hergeleitet werden. Das Proton
besteht aus drei Elektronen, zwei Positronen und einem Negatron. Diese
bewegen sich so schnell umeinander, dass durch deren mittlere
Geschwindigkeit die bekannte „Ruhemasse“ durch die relativistische
Massenzunahme entsteht. Genaueres zu den Bahnen im Abschnitt Proton,
Neutron, Massendefekt. Die mittlere Geschwindigkeit der drei Elektronen
im Proton liegt nur knapp unter c. Sie bewegen sich meist aufeinander zu
oder voneinander weg.
|
|
Masse des Negatrons
|
:
|
me
|
=
|
1 |
|
|
Masse des Positrons
|
:
|
me
|
=
|
1 |
|
|
Masse des Protons
|
:
|
mp
|
=
|
1836,114 me |
|
|
Relative Wurzel
|
:
|
B
|
=
|
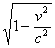 |
|
|
Relative Masse
|
:
|
m
|
=
|
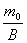 |
|
|
Längenkontraktion
|
:
|
d
|
=
|
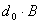 |
|
|
Zeitdilatation
|
:
|
t
|
=
|
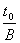 |
|
|
Coloumb-Kraft
|
:
|
FC
|
~
|
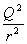 |
|
|
Das ergibt die
Coloumb-Kraft im Proton
|
:
|
FCP
|
=
|
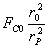 |
|
|
|
:
|
rP
|
=
|
r0×1,634×10-3 |
|
|
|
:
|
FCP
|
=
|
FC0×3,75×105
|
Dadurch spielt
untereinander die relativistische Längenkontraktion eine entscheidende
Rolle. Die Abstände werden untereinander auf das 1,6x10-3
-fache gegenüber dem äußeren Betrachter verringert. In der Formel zur
Berechnung der Kraft steht das Quadrat des Abstandes im Nenner. Somit
wird die Wirkung der Coulombkraft um den Faktor 3,75x105 vergrößert. Das
genügt, um die bekannten Kräfte im Kern zu erklären.
5. Proton, Neutron,
Massendefekt
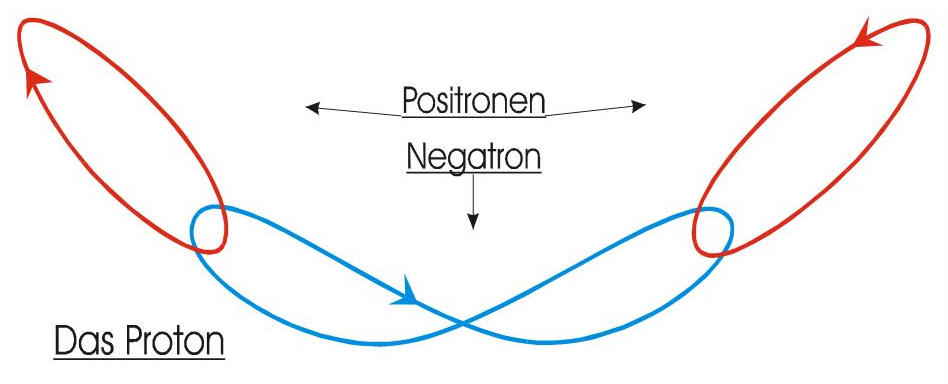
Im Proton
beschreibt das Negatron eine elliptische Acht an deren Enden es jeweils
das entsprechende Positron um einen gemeinsamen Brennpunkt umläuft. Im
unbeeinflussten (energieärmsten) Zustand liegen die Ellipsen der
Positronen in einer Ebene mit der Ebene der Acht, verlaufen aber
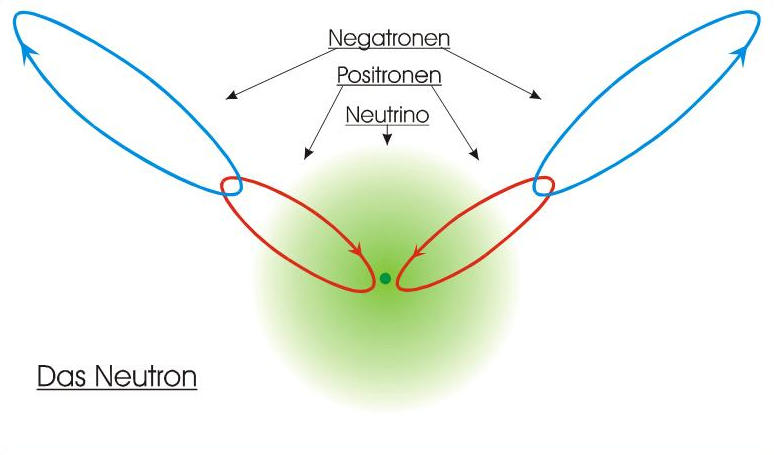
gegensinnig, was dem Spin +0,5 und -0,5 entspricht. Ein Neutron ist ein
Verband aus zwei Negatronen, zwei Positronen und einem Neutrino. Die
beiden Positronen bewegen sich auf elliptischen Bahnen im
Wirkungsbereich des Neutrinos. Sie wirken auf den äußeren Betrachter
durch die Raumkompri-mierung wie ein Teilchen zweifach positiver Ladung.
Um den Brennpunkt der Bahn je eines Positrons bewegen sich die
Negatronen auf ellipsenähnlichen Bahnen synchron in entgegengesetztem
Umlaufsinn, jedoch gleichsinnig mit dem umlaufenen Positron. Die hohen
mittleren Geschwin-digkeiten der beiden Ladungsträgerpaare führen zu
einer relativistischen Massenzunahme und so zur Masse des Neutrons. Die
relativistische Längenkontraktion führt zu einer verstärkten Wirkung der
Coulomb-Kraft. Die relativistische Zeitdilatation führt zu einer
Verlangsamung der Ladungsverschiebungen für einen außenstehenden
Beobachter.
|
Der
Massendefekt kann direkt berechnet werden. Aus der Ruhemasse des
Protons lassen sich die Geschwindigkeit und damit der
Einzelimpuls der sich bewegenden Ladungsteilchen ermitteln. Das
gilt auch für das Neutron, wobei hier die Geschwindigkeit
entscheidend niedriger als im Proton ist. In einem aus Protonen
und Neutronen bestehenden Atomkern bildet sich unter
Berücksichtigung der Impulserhaltung ein neuer Einzelimpuls und
damit eine neue mittlere Geschwindigkeit der Ladungsteilchen.
Daraus lässt sich die exakte Masse eines jeden Isotops
berechnen.
|
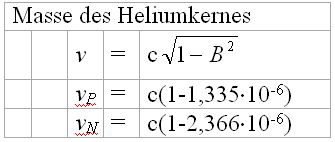 |
Das folgende
Beispiel dient der Berechnung der Masse des Heliumkernes. Aus der Masse
des Protons wird die mittlere Geschwindigkeit der Elektronen des Protons
vP errechnet, aus der des Neutrons die mittlere Geschwindigkeit vN.
Unter Beachtung der Impulserhaltung wird die mittlere Geschwindigkeit
der 14 Elektronen der zwei Protonen und zwei Neutronen des Heliumkernes
vHe errechnet. Daraus ergibt sich die Masse des Heliumkernes als
Vielfaches der Elektronenmasse bzw. in atomaren Masseneinheiten.
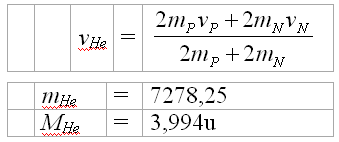
|